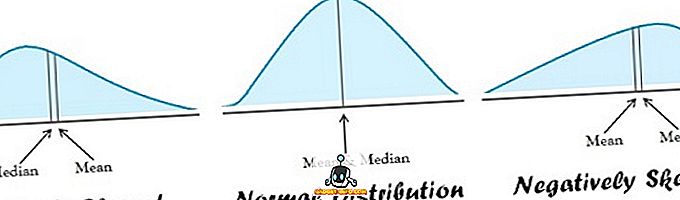
Ukuran ideal kecenderungan utama adalah salah satu yang jelas, mudah difahami, mudah dikalkulasikan. Ia harus berdasarkan semua pemerhatian dan paling kurang dipengaruhi oleh pemerhatian yang melampau hadir dalam set data.
Orang sering membezakan dua langkah ini, tetapi hakikatnya adalah mereka berbeza. Artikel ini secara khusus menyoroti perbezaan asas antara min dan median. Lihatlah.
Carta Perbandingan
| Asas untuk Perbandingan | Maksudnya | Median |
|---|---|---|
| Makna | Maksud merujuk kepada purata purata nilai atau nilai yang ditetapkan. | Median didefinisikan sebagai nombor pertengahan dalam senarai nilai yang diperintahkan. |
| Apa itu? | Ini adalah purata aritmetik. | Ia adalah purata kedudukan. |
| Mewakili | Pusat graviti set data | Pusat graviti set data Set titik pusat data |
| Kebolehgunaan | Pengagihan biasa | Pengedaran tergesa-gesa |
| Pengecualian | Maksudnya adalah sensitif kepada pendengar. | Median tidak sensitif terhadap penglihatan. |
| Pengiraan | Mean dihitung dengan menambahkan semua pemerhatian dan kemudian membahagikan nilai yang diperolehi dengan bilangan pemerhatian. | Untuk mengira median, set data disusun dalam urutan menaik atau menurun, maka nilai yang jatuh di tengah yang tepat dari set data baru, adalah median. |
Definisi Mean
Maksudnya ialah ukuran kecenderungan pusat yang digunakan secara meluas, yang ditakrifkan sebagai purata nilai nilai. Ia mewakili model dan nilai yang paling biasa bagi nilai-nilai yang diberikan. Ia boleh dikira, baik dalam siri yang diskret dan berterusan.
Maksudnya adalah sama dengan jumlah semua pemerhatian dibahagikan dengan bilangan pemerhatian dalam dataset. Jika nilai yang diandaikan oleh pembolehubah adalah sama, maksudnya juga sama. Purata boleh terdiri daripada dua jenis, min sampel (x) dan min populasi (μ). Ia boleh dikira dengan formula yang diberikan:
- Maksud aritmetik :

n = bilangan nilai - Untuk Siri Diskret :

- Untuk Perkhidmatan Berterusan :

A = Assumed Mean
C = Penasihat umum
Definisi Median
Median adalah satu lagi ukuran penting kecenderungan pusat, yang digunakan untuk memisahkan nilai ke dalam dua bahagian yang sama, iaitu lebih separuh daripada sampel, populasi atau pengagihan kebarangkalian dari bahagian bawah. Ia adalah nilai paling menengah, yang dicapai apabila pemerhatian disusun dalam susunan tertentu, sama ada urutan menaik atau menurun.
Untuk pengiraan median, pertama sekali, susunkan pemerhatian yang paling rendah ke tertinggi atau paling tinggi ke tahap terendah, kemudian gunakan formula yang sesuai, mengikut syarat-syarat yang diberikan di bawah:
- Sekiranya bilangan pemerhatian adalah ganjil :

- Sekiranya bilangan pemerhatian adalah :

- Untuk siri berterusan :

c = kekerapan kumulatif kelas median sebelumnya
f = kekerapan kelas median
h = lebar kelas
Perbezaan Utama Antara Mean dan Median
Perbezaan yang signifikan antara min dan median disediakan dalam artikel yang diberikan di bawah:
- Dalam statistik, min ditakrifkan sebagai purata sederhana bagi nilai atau kuantiti yang ditetapkan. Median dikatakan sebagai nombor pertengahan dalam senarai nilai yang diperintahkan.
- Walaupun min adalah purata aritmetik, median adalah purata kedudukan, pada asasnya, kedudukan set data menentukan nilai median.
- Maksudnya menggariskan pusat graviti set data manakala median menyoroti nilai pertengahan paling set data.
- Purata adalah sesuai untuk data diedarkan secara normal. Di hujung yang lain, median adalah yang terbaik apabila pengedaran data menjadi miring.
- Maksudnya sangat terjejas oleh nilai melampau yang tidak berlaku dengan median.
- Maksudnya dikira dengan menambah semua pemerhatian dan kemudian membahagikan nilai yang diperolehi dengan bilangan pemerhatian; hasilnya bermakna. Berbeza dengan median, set data disusun dalam urutan menaik atau turun, maka nilai yang jatuh di tengah yang tepat dari set data baru adalah median.
Contoh
Cari min dan median bagi set data yang diberikan:
58, 26, 65, 34, 78, 44, 96
Penyelesaian: Untuk mengira min, anda perlu membahagikan jumlah pemerhatian dengan jumlah pemerhatian,

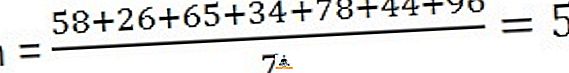
Untuk mengira median, pertama sekali, susunkan siri dalam urutan, iaitu terendah ke tertinggi,
26, 34, 44, 58, 65, 78, 96
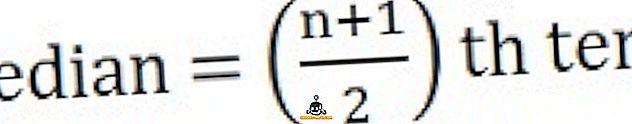
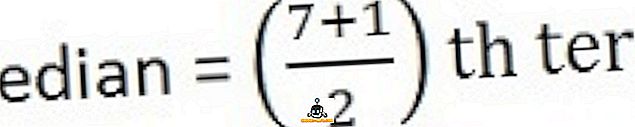
Kesimpulannya
Selepas mengkaji perkara-perkara di atas, kita boleh mengatakan bahawa kedua-dua konsep matematik ini berbeza. Maksud aritmetik atau Mean dianggap sebagai ukuran terbaik dari kecenderungan pusat karena ia mengandung semua ciri ukuran yang ideal tetapi memiliki satu kelemahan yang turun naik sampel mempengaruhi min.
Dengan cara yang sama, median juga jelas jelas dan mudah difahami dan dikira, dan perkara terbaik tentang langkah ini ialah ia tidak terjejas oleh turun naik sampel, tetapi satu-satunya kelemahan median adalah bahawa ia tidak berdasarkan semua pemerhatian. Untuk klasifikasi terbuka, median biasanya lebih disukai berbanding min.